For this exercise we have at our disposal a programmable robotic mower. Our job is to write a software simulation of lawnmowing. It's exceedingly difficult to model the complexities of the physical world with a computer, so we'll make some simplifying assumptions. First, we'll define the lawn as a rectangular area without trees, gardens, rocks, ponds, or cats. (I once saw a solar-powered robot that mowed in a random direction until it bumped into something, at which time it took off in a new, random, direction. Given enough time, it would mow any area completely. I hear these mowers use color/luminance to detect edges, so I guess my cats are safe as long as they don't turn green.) The lawn is also a perfect mowing surface without bumps or undulations, and the grass has uniform thickness; this way we know that the mower can be steered accurately. Finally, we'll assume the mower has a turning radius of zero: that is, it can pivot. (Automatic mowers that are always going forward have a nonzero turning radius.)
To represent the mowing area, we'll use a Perl/Tk canvas widget, colored chlorophyll green of course. Let's assume that to program the mower all we need is to write Perl/Tk code that overlays various items that display the mower's path (lines, arcs, ovals and such) on the canvas, making sure that no green remains. Our first program starts by mowing (drawing a line) 100 feet in a straight line and turning right. It repeats three times until it's mowed the periphery of the lawn. Then the mower shifts right by the width of one cut (I mow clockwise), and repeats the process until there's nothing left to mow.
We'll be creating several variants of the mowing program, so we'll program for reusability by including constants in a module, Mow.pm. This module simply exports a list of variables. It's not object-oriented, although it does inherit some methods from Exporter. Here it is:
# Mow.pm - mowing module. package Mow; use 5.004; use Exporter; @ISA = qw(Exporter); @EXPORT = qw/$CHLOROPHYLL $COLOR $CUT $D2R $PPF $SIDE $TURN/; $CHLOROPHYLL = '#8395ffff0000'; # rye-grass-green, maybe $COLOR = 0xffff; # initial line color $CUT = (38 / 12); # cut width in feet $D2R = 3.14159265 / 180.0; # map degrees to radians $PPF = 2; # pixels/foot $SIDE = 100; # size of square mow area $TURN = (27 / 12); # turn radius in feet 1;
When Perl sees a use Mow statement it populates the program with the variables from the @EXPORT list. With the definitions $CHLOROPHYLL, $CUT, and $SIDE in place (more on 'color numbers' like $CHLOROPHYLL shortly) we can write a simple zero turning radius mowing program.
use Mow;
use Tk;
my $mw = MainWindow->new;
my $canvas = $mw->Canvas(-width => $SIDE,
-height => $SIDE,
-background => $CHLOROPHYLL)->grid;
$mw->waitVisibility;
A chlorophyll green, 100-pixel-square canvas is created and gridded. The waitVisibility() statement forces Tk to display the canvas before the program can proceed, so we can watch the mowing process in real time. Otherwise, the simulation might complete before we could see it. All we need to do now is define a recursive subroutine and call it once:
mow $canvas, 0, 0, $SIDE, $SIDE;
sub mow { # Recursively mow until done.
my($canvas, $x1, $y1, $x2, $y2) = @_;
return if $x1 >= $x2 or $y1 >= $y2;
$canvas->createLine($x1, $y1, $x2, $y1, $x2, $y2,
$x1, $y2, $x1, $y1);
$canvas->idletasks;
$canvas->after(250);
mow $canvas, $x1+$CUT, $y1+$CUT, $x2-$CUT, $y2-$CUT;
} # end mow
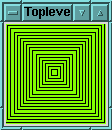
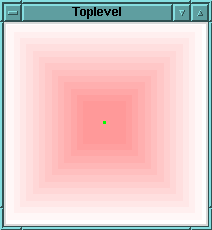
Besides the reference to the canvas, the arguments to mow() are simply coordinates of the top left and bottom right corners of a square. mow() calls the createLine() to paint four line segments - one across the top, right, bottom, and left of the canvas, in that order. Then mow() updates the display and waits a quarter of a second ($canvas->after(250)) before invoking itself again, to mow a smaller square. Here's the not-so-satisfying result:

The main problem is that the width of the cut is pencil thin, so the robot leaves lots of green behind. Luckily, createLine() has some options that help.
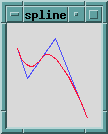
createLine() draws a line between two points. If you provide more than two points, it draws a series of joined line segments. The line segments can even be smoothed using a Bezier spline with the smooth parameter, as this code demonstrates:
my $mw = MainWindow->new;
my $canvas = $mw->Canvas(qw/-width 90 -height 100/)->grid;
$canvas->createLine(qw/10 25 20 55 48 15 80 95 -fill blue/);
$canvas->createLine(qw/10 25 20 55 48 15 80 95
-fill red -smooth yes/);
The ends of a single line segment can be adorned in several ways - with arrowheads (the widget demo, which Tk installs in the same directory as Perl, shows you the arrowheads to choose from), or one of these shapes, called a capstyle:
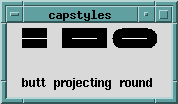
Capstyles become important as the width of the line increases. In the previous picture the fat lines with capstyles were each 25 pixels long and 20 pixels wide. The skinny white lines connect the same canvas points, but have a width of 1 and no capstyle. Notice that the width of the fat items is equally apportioned on each side of the connecting line.
But our mowing program cuts with multiple, fat, and connected line segments, so we need to use another attribute called the joinstyle.
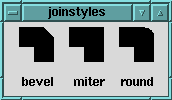
The miter's right angle looks ideal. Finally, fat lines can be filled with a solid color or a stipple. The next version of mow() uses graduated fill colors to highlight the mower's path.
Putting everything together gives us the program below, called zero-tr2 on the TPJ web site.
my $canvas = init;
mow $canvas, (0, 0), ($SIDE, $SIDE);
MainLoop;
sub init {
my $mw = MainWindow->new;
my $mow_side = $SIDE * $PPF;
my $canvas = $mw->Canvas(-width => $mow_side,
-height => $mow_side,
-background => $CHLOROPHYLL)->grid;
$mw->waitVisibility;
return $canvas;
}
sub mow { # Recursively mow until done.
my($canvas, $x1, $y1, $x2, $y2) = @_;
return if $x1 >= $x2 or $y1 >= $y2;
my $color = sprintf("#ffff%04x%04x", $COLOR, $COLOR);
$COLOR -= 0x0800;
$canvas->createLine($x1 * $PPF, $y1 * $PPF,
$x2 * $PPF, $y1 * $PPF,
$x2 * $PPF, $y2 * $PPF,
$x1 * $PPF, $y2 * $PPF,
$x1 * $PPF, $y1 * $PPF,
-width => $CUT * $PPF + 0.5, -fill => $color,
-joinstyle => 'miter');
$canvas->idletasks;
$canvas->after(250);
mow $canvas, $x1+$CUT, $y1+$CUT, $x2-$CUT, $y2-$CUT;
} # end mow
Four comments:
Let's complicate matters and assume our robot is in the shop for repairs. We have an older model with a nonzero turning radius; that is, it turns with an arc, leaving a small swath of green behind. To simulate this, the mowing program could draw connected lines and arcs for each side of the mowing area. While these eight items are still manageable, it might be easier to define one line and one arc, and have mow() rotate them as required.
Rotating a line in a Cartesian coordinate space is simple if one of the endpoints is at (0, 0). Then the rotation reduces to rotating the other endpoint. Given such a point (x,y), we can rotate it through the angle q using these equations:
x' = x cos q – y sin q
y' = x sin q + y cos q
(x', y') is the new location of the point.
Rotating a line about an arbitrary point requires that the line be translated to the origin, rotated, and then translated back to its original location. The following code rotates (clockwise) the line whose endpoints are (0,0) and (20,40) about the center point of the canvas, (65,65). It draws a line and then creates an invisible bounding rectangle. We'll employ one of those shortly to define an oval for the turning radius arc.
my $mw = MainWindow->new;
my $canvas = $mw->Canvas(-width => 130, -height => 130)->grid;
$mw->waitVisibility;
my $origin = 65; # origin of canvas
my($x2, $y2) = (20, 40); # endpoint of line segment
rotate $canvas, 0, $x2, $y2, 'black';
rotate $canvas, 90, $x2, $y2, 'red';
rotate $canvas, 180, $x2, $y2, 'green';
rotate $canvas, 270, $x2, $y2, 'blue';
MainLoop;
sub rotate {
my($canvas, $theta, $x2, $y2, $color) = @ARG;
$theta *= $D2R; # degrees to radians
my $nx2 = $x2 * cos($theta) - $y2 * sin($theta);
my $ny2 = $x2 * sin($theta) + $y2 * cos($theta);
$canvas->createLine (0+$origin, 0+$origin, $nx2+$origin,
$ny2+$origin, -fill => $color);
$canvas->createRectangle(0+$origin, 0+$origin,
$nx2+$origin, $ny2+$origin, -outline => $color);
my $coords = sprintf("(%d,%d)", int($nx2), int($ny2));
$canvas->createText ($nx2+$origin, $ny2+$origin,
-text => $coords, -font => 'fixed');
$canvas->idletasks;
$canvas->after(250);
} # end rotate
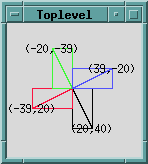
The previous code introduced two new canvas items: rectangle and text. Like the mowing area, two diagonally opposed corners define a rectangle (here, the endpoints of the rotating line segment). You can't do much else with a rectangle other than specify the width and color of its outline, or fill it with a color or stipple.
The canvas text item annotates the business end of a line with its coordinates (the other endpoint is always (0,0)). These floating point values are truncated without rounding, which is why some of the numbers are a bit off. Text items can be anchored, justified and filled, as you'd expect. There are methods to insert and delete characters, too.
The tools for the next mowing program are now at hand. We can take a line and rotate it through an arbitrary angle and draw it anywhere on the canvas. We can also use the two points that define a line and draw a rectangle instead, at any angle, anywhere on the canvas. And since an arc is defined by an oval which is defined by a bounding rectangle, we can rotate and draw an arc anywhere on the canvas.
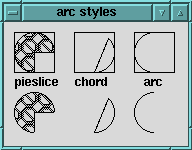
The three different arc styles were created with the following statements. The first four elements represent the bounding boxes:
$canvas->createArc(qw/10 10 50 50 -start 0 -extent 270
-style pieslice -fill black -stipple error/)
;
$canvas->createArc(qw/70 10 110 50 -start 45 -extent -135
-style chord/);
$canvas->createArc(qw/130 10 170 50 -start -90 -extent -180
-style arc/);
Each arc has a starting angle and an extent, both in degrees, with zero degrees along the x-axis. Positive angles rotate counterclockwise and negative angles clockwise. The pie slice arc is stipple filled with a Tk built-in bitmap.
The new controller code starts by defining two points: an endpoint of a line, and one corner of the arc's bounding box. The point (0,0) doubles as the line's other endpoint, as well as the opposite corner of the arc's bounding box. The bounding box is square because the mower's circular turning radius must fit inside.
@LINE = ($SIDE, 0); # initial straight line mowing path @ARC = ($TURN, $TURN); # generic turning radius arc
The change to mow(): it now rotates the line and arc, computes three points, and then draws the two items (the full program is called nz-tr1). Points one and two are the line's endpoints; points two and three are the arc's bounding box. Thus, the end of the line and the start of the arc coincide. Here's an excerpt:
$canvas->createLine($start[0], $start[1], $end[0], $end[1],
-fill => $color, -width => $CUT,
-capstyle => 'round', -tags => 'path');
($x2, $y2) = @ARC[0,1];
$nx2 = $x2 * cos($theta) - $y2 * sin($theta);
$ny2 = $x2 * sin($theta) + $y2 * cos($theta);
$canvas->createArc($end[0], $end[1], $end[0]+$nx2, $end[1]+$ny2,
-start => 270-20-$angle, -extent => 180+40,
-style => 'arc', -outline => $color,
-width => $CUT, -tags => 'path');
This simulation produces the same visible results as the zero turning radius code.
The previous snippet demonstrates tags, a powerful canvas concept. Tags are simply strings used to identify canvas items, which you add or delete as needed. A canvas item can have any number of tags, and the same tag can be applied to any number of items. The mowing program uses the path tag to group all the lines and arcs that define the mowing path. (Every canvas item has at least one tag, the string all.)
Tags are supplied to canvas methods to select which items to operate upon; for example, this binding turns all fat lines and arcs into skinny lines and arcs. This allows the green canvas background to show through:
$canvas->CanvasBind('<Double-1>' => sub {
$canvas->itemconfigure('path', -width => 1)
});
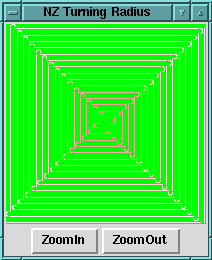
A canvas can also be scaled to implement a primitive zoom function. Scaling adjusts each of the points defining an item by changing the points' distance from an origin by the scale factor. For example, this code uses the middle of the canvas as the origin and doubles the X and Y coordinates of all items tagged with the string path. Scaling doesn't affect the line width, however.
my $origin = $SIDE / 2;
my $zi = $zf->Button(qw/-text ZoomIn -command/ =>
[$canvas => 'scale', 'path',
$origin, $origin, 2.0, 2.0]);
After a few presses of the ZoomIn button we see this detail:
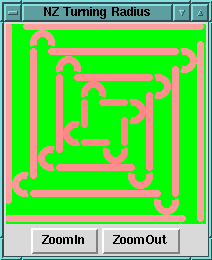
I can't mow as nicely as the robot. As I turn my tractor it continues to move forward, so the turning arc isn't circular but almost teardrop in shape. My mowing surface is sloping and bumpy, and I don't always start and finish turns at the same time. So no two turns are identical. My sloppiness often leads to uncut grass, as illustrated here:
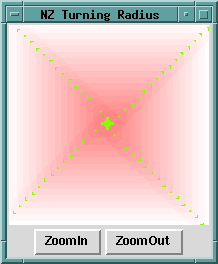
I realized this was more like reality, and the global view of the situation gave me an idea. Modifying the program, I used two lines to paint a large X on the canvas, and a few trials later found that this code sufficed to cut the remaining grass:
$canvas->createLine(0, 0, $SIDE, $SIDE,
-width => (2 * $CUT)+0.5, -fill => 'yellow');
$canvas->createLine($SIDE, 0, 0, $SIDE,
-width => (2 * $CUT)+0.5, -fill => 'yellow');
So the magic number was two mower widths, a trip up and back each diagonal. Last year I went out and performed the experiment, and the results agreed nicely with theory: my magic number was three: a trip up, back, and up each diagonal.
_ _END_ _